题目
试题一(15分)
阅读以下说明和流程图,填写流程图中的空缺,将解答填入答题纸的对应栏内。
【说明】
对于大于1的正整数n,(x+1)n可展开为
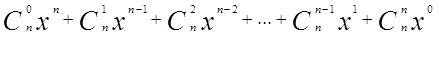
下面流程图的作用是计算(x+1)n展开后的各项系数
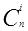 (i=0,1,....,n)并依次存放在数组A[0...n]中。方法是依次计算k=2,3,..,n时(x +1)k的展开系数并存入数组A,在此过程中,对任一确定的k,利用关系式
(i=0,1,....,n)并依次存放在数组A[0...n]中。方法是依次计算k=2,3,..,n时(x +1)k的展开系数并存入数组A,在此过程中,对任一确定的k,利用关系式
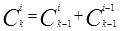 ,按照i递减的顺序逐步计算并将结果存储在数组A中。其中,
,按照i递减的顺序逐步计算并将结果存储在数组A中。其中,
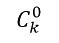 和
和
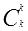 都为1,因此可直接设置A[0]、A[k]的值为1。
都为1,因此可直接设置A[0]、A[k]的值为1。
例如,计算(x+1)3的过程如下:
先计算 (x+1)2 ( 即k=2) 的各项系数,然后计算(x+1)3(即k=3)的各项系数。
K=2时,需要计算
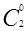 ,
,
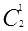 和
和
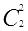 ,并存入A[0] ,A[1]和A[2],其中A[0]和A[1]的值已有,因此将
,并存入A[0] ,A[1]和A[2],其中A[0]和A[1]的值已有,因此将
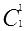 (即 A[1])和
(即 A[1])和
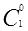 即 (A[0])相加得到
即 (A[0])相加得到
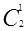 的值并存入A[1]。
的值并存入A[1]。
k=3 时,需要计算
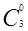 ,
,
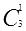 和
和
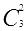 和
和
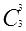 ,先计算出
,先计算出
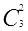 (由
(由
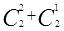 )得到并存入A[2],再计算
)得到并存入A[2],再计算
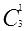 (由
(由
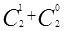 得到)并存入A[1]。 【流程图】
得到)并存入A[1]。 【流程图】
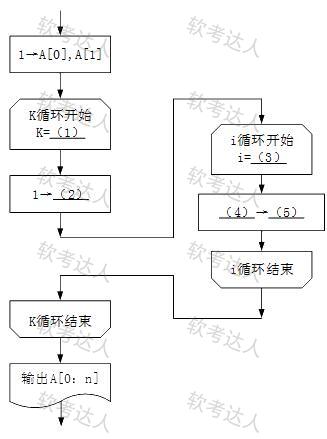
注:循环开始框内应给出循环控制变量的初值和终值,默认递增值为1。
格式为:循环控制变量=初值,终值,递增值。
【问题1】(15分)
(1):
(2):
(3):
(4):
(5):
阅读以下说明和流程图,填写流程图中的空缺,将解答填入答题纸的对应栏内。
【说明】
对于大于1的正整数n,(x+1)n可展开为
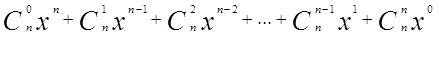
下面流程图的作用是计算(x+1)n展开后的各项系数
例如,计算(x+1)3的过程如下:
先计算 (x+1)2 ( 即k=2) 的各项系数,然后计算(x+1)3(即k=3)的各项系数。
K=2时,需要计算
k=3 时,需要计算

注:循环开始框内应给出循环控制变量的初值和终值,默认递增值为1。
格式为:循环控制变量=初值,终值,递增值。
【问题1】(15分)
(1):
(2):
(3):
(4):
(5):

作答
本题暂不支持做答,请点击“解析“以对比解题思路
答案/解析
查看试卷及答案


