【软考达人-回忆版】
试题四(共15分)
阅读下列说明和C代码,回答问题I至问题3,将解答写在答题纸的对应栏内。
【说明】
工程计算中经常要完成多个矩阵相乘的计算任务,对矩郑相乘进行以下说明。
( )两个矩阵相乘要求第一个矩阵 的列数等于第二个矩阵的行数,计算量主要由进行乘法运算的次数决定,假设采用标准的矩阵相乘算法,计算Amxn*Bxp"需要m*n*p次行乘法运算的次数决定、乘法运算,即时间复杂度为O(m*n*p).
( )矩阵相乘满足结合律,多个矩阵相乘时不同的计算顺序会产生不同的计算量。以矩阵Al5×100,A2100*8,A38×50三个矩阵相乘为例,若按(A1*A2)*A3计算,则需要进行 5*100*8+5*8*50-6000 次乘法运算;若按 A1*(A2*A3)计算,则需要进行100*8*50+5*100*50=65000次乘法运算。
陌阵链乘问题可描述为∶给定n个矩阵
对较大的n,可能的计算顺序数量非常庞大,用蛮力法确定计算顺序是不实际的。经过对问题进行分析,发现矩阵链乘问题具有最优子结构,即若 A1*A2*…*An的一个最优计算顺序从第k个矩阵处断开,即分为 A1*A2*…*Ak 和Ak+1*Ak+2*…*An 两个子问题,则该最优解应该包含 A1*A2*…*Ak 的一个最优计算顺序和 Ak+1*Ak+2*…*An的一个最优计算顺序。据此构造递归式,
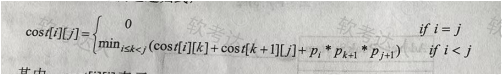
其中,cost【jj】表示 Ai+1*Ai+2**Aj+1 的最优计算的计算代价。最终需要求解cost[O][n-1]。【C代码】
算法实现采用自底向上的计算过程。首先计算两个矩阵相乘的计算量,然后依次计算个矩阵、4个矩阵、……、n个矩阵相乘的最小计算量及最优计算顺序。下面是该算法的语言实现。
( )主要变量说明n∶矩阵数seq【】∶矩阵维数序列
cos【J【∶二维数组,长度为n*n,其中元素cost【】□】表示 Ai+1*Ai+2*…*Aj+1的最优的计算代价
race【0∶二维数组,长度为n*n,其中元素 trace【i】【】 表示Ai+1*Ai+2*…*Aj+1的最算对应的划分位置,即k
( )函数cmm ine N 100 ost[N[N];

return cost[0][n-1];
【问题3】(3分)
考虑实例n=4,各个矩阵的维数为A1为15*5,A2为5*10,A3为10*20,A4为20*25,即维度序列为15,5,10,20和25。则根据上述C代码得到的一个最优计算顺序为_( )(用加括号方式表示计算顺序),所需要的乘法运算次数为_( )
【软考达人-回忆版】
试题四(共15分)
阅读下列说明和C代码,回答问题I至问题3,将解答写在答题纸的对应栏内。
【说明】
工程计算中经常要完成多个矩阵相乘的计算任务,对矩郑相乘进行以下说明。
( )两个矩阵相乘要求第一个矩阵 的列数等于第二个矩阵的行数,计算量主要由进行乘法运算的次数决定,假设采用标准的矩阵相乘算法,计算Amxn*Bxp"需要m*n*p次行乘法运算的次数决定、乘法运算,即时间复杂度为O(m*n*p).
( )矩阵相乘满足结合律,多个矩阵相乘时不同的计算顺序会产生不同的计算量。以矩阵Al5×100,A2100*8,A38×50三个矩阵相乘为例,若按(A1*A2)*A3计算,则需要进行 5*100*8+5*8*50-6000 次乘法运算;若按 A1*(A2*A3)计算,则需要进行100*8*50+5*100*50=65000次乘法运算。
陌阵链乘问题可描述为∶给定n个矩阵
对较大的n,可能的计算顺序数量非常庞大,用蛮力法确定计算顺序是不实际的。经过对问题进行分析,发现矩阵链乘问题具有最优子结构,即若 A1*A2*…*An的一个最优计算顺序从第k个矩阵处断开,即分为 A1*A2*…*Ak 和Ak+1*Ak+2*…*An 两个子问题,则该最优解应该包含 A1*A2*…*Ak 的一个最优计算顺序和 Ak+1*Ak+2*…*An的一个最优计算顺序。据此构造递归式,
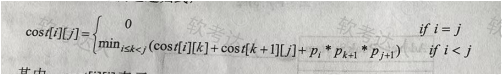
其中,cost【jj】表示 Ai+1*Ai+2**Aj+1 的最优计算的计算代价。最终需要求解cost[O][n-1]。【C代码】
算法实现采用自底向上的计算过程。首先计算两个矩阵相乘的计算量,然后依次计算个矩阵、4个矩阵、……、n个矩阵相乘的最小计算量及最优计算顺序。下面是该算法的语言实现。
( )主要变量说明n∶矩阵数seq【】∶矩阵维数序列
cos【J【∶二维数组,长度为n*n,其中元素cost【】□】表示 Ai+1*Ai+2*…*Aj+1的最优的计算代价
race【0∶二维数组,长度为n*n,其中元素 trace【i】【】 表示Ai+1*Ai+2*…*Aj+1的最算对应的划分位置,即k
( )函数cmm ine N 100 ost[N[N];

return cost[0][n-1];
【问题3】(3分)
考虑实例n=4,各个矩阵的维数为A1为15*5,A2为5*10,A3为10*20,A4为20*25,即维度序列为15,5,10,20和25。则根据上述C代码得到的一个最优计算顺序为_( )(用加括号方式表示计算顺序),所需要的乘法运算次数为_( )



